Question

Which of the following could be the lengths of the sides of a 45°-45°-90° triangle?

Answer 1

Answers B and D

Explanation:

The side lengths must satisfy the Pythagorean Theorem: a² + b² = c²

Note that in Answer D, 3² + 4² = 5² (or 9 + 16 = 25).

Also: In Answer B, (3√2)² + 3√2)² = 6² (or 18 + 18 = 36)

Answer 2

option B

Explanation:

since two two angles are 45 degree it can be said that the other two smaller legs of a triangle are equal.

Hypotenuse is 90 degree because it is opposite of 90 degree (which is a largest angle).

out of these four options A and B are the possible answers.because its two sides are equal. Now we should check which one is correct by using pythagoras theorem.

for option A

a^2 + b^2 = c^2

`((√(3) )/(2) )^2` +
`((√(3) )/(2))^2` =
`\sqrt{√(2) }`

`(3)/(4) + (3)/(4) = 2`

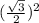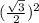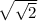
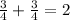
take lcm of denominator

`(3+3)/(4) =2`

`(6)/(4)=2`

`(3)/(2 ) =2`

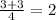
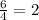
this can not be the sides of the right angle because according to the pythagoras theorem to be the right angle sum of square of two smaller sides of a triangle must equal to the square of hypotenuse .But here it is not equal.so it cannot be the sides of right angle triangle.

For option B

a^2 + b^2 = c^2

`(3√(2) )^2 + (3√(2))^2 = 6^2`

`3*3*2 + 3*3*2 =36`

`18 + 18 =36`

`36 = 36`

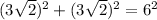
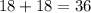
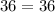
since both sides are equal it satisfies the pythagoras theorem.

therefore answer is option B.