Answer:
The least prize size G that I will be willing to buy the lottery is 192
Step-by-step explanation:
First, Calculate the expected utility
Expected utility =
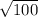 = 10
= 10
There are two cases
Case 1
I win = 100 - 36 + G = 64 + G
Case 2
I lose = 100 - 36 = 64
Hence the expected utility can be calculated as follow
Expected utility = Chance to win x
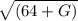 + Chance to lose x
+ Chance to lose x
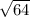
10 = 25% x
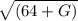 + ( 100% - 25% ) x
+ ( 100% - 25% ) x
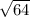
10 = 25% x
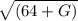 + 75% x 8
+ 75% x 8
10 = 25% x
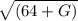 + 6
+ 6
10 - 6 = 25% x
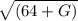
4 = 25% x
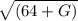
4 / 25% =
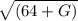
16 =
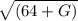
 =
=
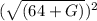
256 = 64 + G
G = 256 - 64
G = 192