Question

Three unit squares (1-by-1 squares) and two line segments connecting two pairs of vertices are shown.

What is the area of AABC?

Answer 1

Explanation:

I don't know if, just because I'm a high school math teacher, I way over-think things, but the method I used to come to the answer here is crazy and convoluted...but it works. Follow me here while I explain it.

I put that drawing you have there in a coordinate plane and made a point D at the end of the segment that begins with A; made a point E at the end of the segment that begins with B. Putting that into a coordinate plane with E at the origin gives A coordinates of (0, 2); B (1, 2); D (2, 1). We need to find the coordinates of C to use later. That's the first job.

When you put this into a coordinate plane, it allows you to write the equations of the segments AD and BE.

AD: y = -1/2x + 2

BE: y = 2x

If you set these equal to each other, you can see where the lines intersect (the coordiantes of this point) by solving for x and y.

-1/2x + 2 = 2x and

2.5x = 2 so

x = .8

And if x = .8, we can sub that into either equation to find y:

y = 2(.8) so

y = 1.6

So the coordinates of C are (.8, 1.6).

Now we can find the lengths of each of these segments AC and BC. We already know that the length of segment AB is 1.

Find the lengths of each of these segments using the coordinates for each in the distance formula. The lengths are as follows:

AC = .8944

BC = .4472

This allows me to use the Law of Cosines to find the measure of angle A.

Angle A = 26.56°

Now I can use the area formula for a triangle that says

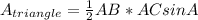`A_(triangle)=(1)/(2)AB*ACsinA` and

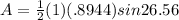`A=(1)/(2)(1)(.8944)sin26.56` so

A = .1999 units squared