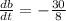Answer:
The base reduces at 3.75cm/min
Explanation:
Given
Let
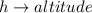
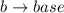
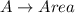
So:
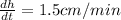
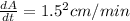
The area of a triangle is:
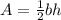
Calculate b when
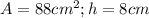
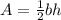

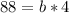
Solve for b

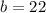
We have:
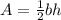
Differentiate with respect to time
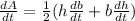
Substitute the following values in the above equation
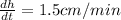
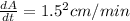
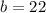

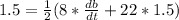
Multiply both sides by 2
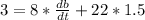
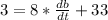
Collect like terms
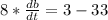
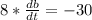
Divide both sides by 8