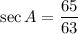Question

Given csc(A) = 60/16 and that angle A is in Quadrant I, find the exact value of sec A in simplest radical form using a rational denominator . Someone please help me!

Answer 1

Explanation:

cosec A =60/16

hypotenuse/opposite = 60/16 =15/4 (in simplest form)

therefore hypotenuse = 15 , opposite = 4

then adjacent =? (let be x)

using pythagoras theorem to find adjacent

opposite^2 + adjacent^2 = hypotenuse^2

4^2 + x^2 = 15^2

16 + x^2 = 225

x^2 = 225 - 16

x^2 = 209

`x=√(209)`

sec A =hypotenuse/adjacent

`=(15)/(√(209) )`

`=(15)/(√(209) ) * (√(209) )/(√(209) )`

=
`(15√(209) )/(209)`

Answer 2

`\displaystyle \sec A=(65)/(63)`

Explanation:

We are given that:

`\displaystyle \csc A=(65)/(16)`

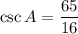
Where A is in QI.

And we want to find sec(A).

Recall that cosecant is the ratio of the hypotenuse to the opposite side. So, find the adjacent side using the Pythagorean Theorem:

`a=√(65^2-16^2)=√(3969)=63`

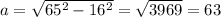
So, with respect to A, our adjacent side is 63, our opposite side is 16, and our hypotenuse is 65.

Since A is in QI, all of our trigonometric ratios will be positive.

Secant is the ratio of the hypotenuse to the adjacent. Hence:

`\displaystyle \sec A=(65)/(63)`