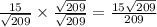Question

Given csc(A) = 60/16 and that angle A is in Quadrant I, find the exact value of sec A in simplest radical form using a rational denominator . Someone please help me!

Answer 1

`(15 √(209) )/(209)`

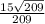
Explanation:

Objective: Understand and work with trig identies.

Recall multiple trig identies and manipulate them to get from cosecant to secant.

Given

`\csc(a) = (60)/(16)`

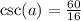
Apply reciprocal identity csc a = 1/sin a.

`\sin(a) = (16)/(60)`

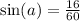
Apply pythagorean identity to find cos a.

`( (16)/(60)) {}^(2) + \cos(x) {}^(2) = 1`

`(256)/(3600) + \cos(x) {}^(2) = 1`

`\cos(x) {}^(2) = (3600)/(3600) - (256)/(3600)`

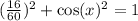
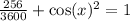
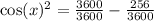
We can simplify both expression

`\cos(x) {}^(2) = (225)/(225) - (16)/(225)`

`\cos(x) = ( √(209) )/(15)`

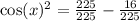
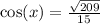
Cosine is positve on quadrant 1 so that cos(a)

Apply reciprocal identity sec a= 1/ cos a.

The answer is

`\sec(a) = (15)/( √(209) )`

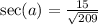
Rationalize the denominator.

`(15)/( √(209) ) * ( √(209) )/( √(209) ) = (15 √(209) )/(209)`