Question

A gymnast of mass 65 kg bounces vertically on a trampoline so that

she approaches and leaves the trampoline with a speed of 10 m/s and
contact time of 0.9 s. Calculate (1) her change of momentum (ii) the
average resultant force exerted on her while in contact with the
trampoline​

Answer 1

The change in momentum of the gymnast is 1300 kg·m/s, and the average resultant force exerted on the gymnast while in contact with the trampoline is approximately 1444.44 N.

Step-by-step explanation:

The student's question regarding the momentum change and average force exerted on a gymnast bouncing on a trampoline involves concepts from classical mechanics in physics. To solve this problem, we first calculate the gymnast's change in momentum. The momentum of an object is given by the product of its mass and velocity. Since the gymnast approaches and leaves the trampoline at 10 m/s, the change in velocity is 10 m/s (upward) - (-10 m/s) (downward) = 20 m/s. Therefore, the change in momentum (Δp) is:

Δp = mass × change in velocity = 65 kg × 20 m/s = 1300 kg·m/s.

To find the average resultant force exerted on the gymnast, we use the impulse-momentum theorem, which states that the impulse is equal to the change in momentum. The impulse is also equal to the average force multiplied by the contact time, so:

Average force = Δp / contact time = 1300 kg·m/s / 0.9 s = approximately 1444.44 N.

Answer 2

Change in momentum:
`1.3 * 10^(3)\;\rm kg \cdot m \cdot s^(-1)`

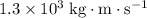
Average resultant force: approximately
`1.4 * 10^(3)\; \rm N`.

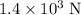Step-by-step explanation:

Consider an object of mass
`m` travelling at velocity
`v`. The momentum of this object would be
`p = m \cdot v`.

Momentum is a vector. The direction of an object's momentum is the same as the direction of its velocity.

Initial velocity of this gymnast:
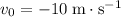`v_0 = -10\; \rm m \cdot s^(-1)`. This value is negative because the gymnast was initially travelling downwards.

Hence, the initial momentum of this gymnast would be:

`\begin{aligned}p_0 &= m \cdot v_0 \\ &= 65\; \rm kg * (-10\; \rm m \cdot s^(-1))\\ &= -650\; \rm kg \cdot m \cdot s^(-1)\end{aligned}`.

Velocity of this gymnast after leaving the trampoline:
`v_1 = 10\; \rm m\cdot s^(-1)`.

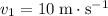Hence, the momentum of this gymnast when leaving the trampoline would be:

`\begin{aligned}p_1 &= m \cdot v_1 \\ &= 65\; \rm kg * 10\; \rm m \cdot s^(-1)\\ &= 650\; \rm kg \cdot m \cdot s^(-1)\end{aligned}`.

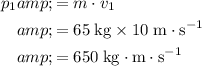Change in momentum:

`\begin{aligned}&p_1 - p_0 \\ &= 650\; \rm kg \cdot m \cdot s^(-1) - (-650\; \rm kg \cdot m \cdot s^(-1)) \\ &= 1300\; \rm kg \cdot m\cdot s^(-1)\end{aligned}`.

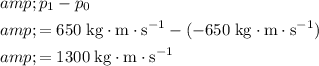By Newton's Second Law of motion, if the momentum of an object changed by
`\Delta p` over time
`t`, the average net force on that object would be:

`\begin{aligned}F &= (\Delta p)/(t)\end{aligned}`.

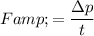For this gymnast:

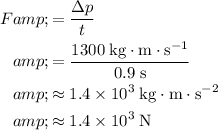`\begin{aligned}F&= (\Delta p)/(t) \\ &= (1300\; \rm kg \cdot m \cdot s^(-1))/(0.9\; \rm s) \\ &\approx 1.4 * 10^(3)\; \rm kg \cdot m \cdot s^(-2) \\ &\approx 1.4 * 10^(3)\; \rm N\end{aligned}`.