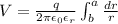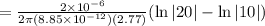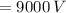Question

I'm struggling on calculus. PLEASE HELP ASAP. use red writing to help out.​

Answer 1

Explanation:

1. Given: a = 4t + 4

We know that

`a = (dv)/(dt) \: \: or \: dv = adt`

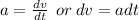
By definition, the integral of a power function x^n is

`\int {x}^(n) dx = \frac{ {x}^(n + 1) }{n + 1} + k`

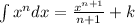
Integrating the acceleration a, we get

`v = \int adt = \int(4t + 4)dt = 2 {t}^(2) + 4t + k`

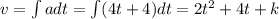
where k = constant of integration. We know that v = 10 when t = 0 so when we do the substitution, we get k = 10 therefore, the final expression for v is

`v = 2 {t}^(2) + 4t + 10`

To find s, we need to integrate v. Knowing that

`v = (ds)/(dt) \: \: or \: s = \int v \: dt`

`s = \int(2 {t}^(2) + 4t + 10)dt`

`= (2)/(3) {t}^(3) + 2 {t}^(2) + 10t + k`

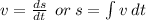
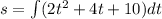
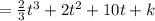
where k once again is the constant of integration. We know that s = 2 when t = 0, which gives us k = 2. Therefore, the final expression for s is

`s = (2)/(3) {t}^(3) + 2 {t}^(2) + 10t + 2`

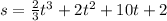
2. The potential difference V between two boundaries a and b is given by

`V = (q)/(2\pi \epsilon_0 \epsilon_r) \int_(b)^(a) (dr)/(r)`

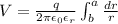
Note that the integral in the expression above can be rewritten and the integrated as

`\int_(b)^(a) (dr)/(r) =\int_(b)^(a) {r}^( - 1) dr = \ln |a| - \ln |b|`

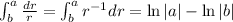
so the potential difference V is then J

`V = (q)/(2\pi \epsilon_0 \epsilon_r) \int_(b)^(a) (dr)/(r)`

`= \frac{2 * {10}^( - 6) }{2\pi (8.85* {10}^( - 12)) (2.77)}( \ln |20| - \ln |10| )`

`= 9000 \: V`