Question

The height of a ball kicked in the air is modeled by the equation h(t) = -2t^2 +8t +24, where h is the height of the ball in feet and t is the time in seconds. What is the average rate of change of the function over the intervalt t = 2 to t = 5

A. -3

B. -6

C. 3

D. 6

Answer 1

Explanation:

The rate of change in any function is the slope of the line between 2 points. Our points are t = 2 and t = 5. But we know that the slope formula also involves the h's for each of those t's. We need to find them first. The slope formula is

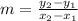`m=(y_2-y_1)/(x_2-x_1)`, but for us it will look like this (fittted to our needs):

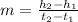`m=(h_2-h_1)/(t_2-t_1)`. So we need to find those h's.

when t = 2, plug in a 2 for t and solve for h.

Therefore,
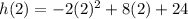`h(2)=-2(2)^2+8(2)+24` and

h(2) = 32 and in coordinate form, (2, 32).

When t = 5, plug in a 5 for t and solve for h.

Therefore,
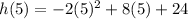`h(5) =-2(5)^2+8(5)+24` and

h(5) = 14 and in coordinate form, (5, 14). Now we can plug into our slope formula:

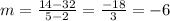`m=(14-32)/(5-2)=(-18)/(3)=-6` , choice B.

The rate of change is -6 which, in words, means that the ball fell 6 feet every 1 second it fell.