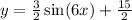Answer:
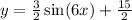
Explanation:
Given
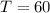 --- period
--- period
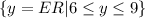 --- range
--- range
Required
The sine function
A sine function is represented as:
![y = A\sin[k(x - d)] + c](https://img.qammunity.org/2022/formulas/mathematics/high-school/mqijwm0z126ywokx0xc1p0cpkji2q9x677.png)
Where:

and

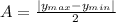
and
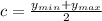
Given that the range is:
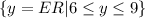
This implies that:


So, we have:
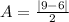

Remove absolute bracket
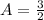
Next, calculate k


Make |k| the subject
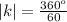
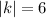
Remove absolute bracket
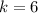
Next, calculate c
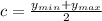
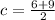
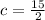
So, we have:
![y = A\sin[k(x - d)] + c](https://img.qammunity.org/2022/formulas/mathematics/high-school/mqijwm0z126ywokx0xc1p0cpkji2q9x677.png)
![y = (3)/(2)\sin[6(x -d)] + (15)/(2)](https://img.qammunity.org/2022/formulas/mathematics/high-school/llp6uzhrtlc21kd1kevgrfc7fzvz37s28y.png)
Set d to 0