Question

Given that f(x) = √(ax + 1) , with x ≥ -1/a and a > 0

and g(x) = (x+1)/x, with x ≠ 0.
if ( f~¹ • g~¹) (3) = -⅜ ,
find : a²+ 3a -3 !​

Answer 1

`\displaystyle 7`

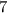
Explanation:

first thing I assume by f~¹ you meant
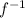`f^(-1)` however

we want to find a²+3x-3 for the given condition. with the composite function condition we can do so

Finding the inverse of f(x):

`\displaystyle f(x) = √(ax + 1)`

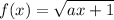
substitute y for f(x):

`\displaystyle y= √(ax + 1)`

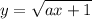
interchange:

`\displaystyle x= √(ay + 1)`

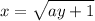
square both sides:

`\displaystyle ay + 1 = {x}^(2)`

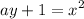
cancel 1 from both sides:

`\displaystyle ay = {x}^(2) - 1`

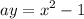
divide both sides by a:

`\displaystyle y = \frac{{x}^(2) - 1 }{a}`

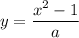
substitute f^-1 for y:

`\displaystyle f ^( - 1) (x) = \frac{{x}^(2) - 1 }{a}`

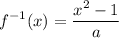
finding the inverse of g(x):

`\displaystyle g(x) = (x + 1)/(x)`

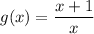
substitute y for g(x)

`\displaystyle y= (x + 1)/(x)`

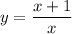
interchange:

`\displaystyle (y + 1)/(y) =x`

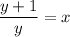
cross multiplication

`\displaystyle y + 1= xy`

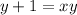
cancel 1 from both sides

`\displaystyle y - xy= - 1`

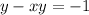
factor out y:

`\displaystyle y(1 - x)= - 1`

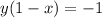
divide both sides by 1-x:

`\displaystyle y= - (1)/( 1 - x)`

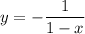
substitute g^-1 for y:

`\displaystyle g ^( - 1) (x)= - (1)/( 1 - x)`

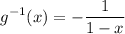
remember that

`\displaystyle (f \circ g)x = f(g(x))`

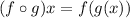
therefore we obtain:

`\rm \displaystyle (f ^( - 1) \circ g ^( - 1) ) (3) = \frac{{ \bigg(- (1)/(1 - 3) } \bigg)^(2) - 1 }{a}`

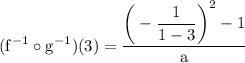
since (f~¹•g~¹)(3)=-⅜ thus substitute:

`\rm \displaystyle \frac{{ \bigg(- (1)/(1 - 3) } \bigg)^(2) - 1 }{a} = - (3)/(8)`

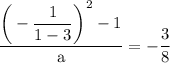
simplify parentheses:

`\rm \displaystyle \frac{{ \bigg( (1)/(2) } \bigg)^(2) - 1 }{a} = - (3)/(8)`

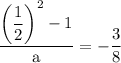
simplify square:

`\rm \displaystyle \frac{{ (1)/(4) } - 1 }{a} = - (3)/(8)`

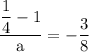
simplify substraction:

`\rm \displaystyle ( - (3)/(4) )/( a)= - (3)/(8)`

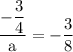
simplify complex fraction:

`\rm \displaystyle - (3)/(4a) = - (3)/(8)`

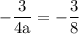
get rid of - sign:

`\rm \displaystyle (3)/(4a) = (3)/(8)`

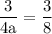
divide both sides by 3:

`\rm \displaystyle (1)/(4a) = (1)/(8)`

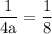
cross multiplication:

`\rm \displaystyle 4a= 8`

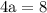
divide both sides by 4:

`\rm \displaystyle \boxed{ a= 2}`

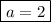
as we want to find a²+3a-3 substitute the got value of a:

`\displaystyle {2}^(2) + 3.2 - 3`

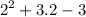
simplify square:

`\displaystyle 4 + 3.2 - 3`

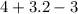
simplify multiplication:

`\displaystyle 4 +6 - 3`

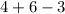
simplify addition:

`\displaystyle 10 - 3`

simplify substraction:

`\displaystyle 7`

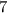
and we are done!