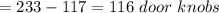Question

In a continuous review inventory​ system, the lead time for door knobs is weeks. The standard deviation of demand during the lead time is units. The desired​ cycle-service level is percent. The supplier of door knobs streamlined its operations and now quotes a 1 week lead time. Refer to the standard normal tableLOADING... for​ z-values. How much can the safety stock be reduced without reducing the percent​ cycle-service level? The safety stock can be reduced by nothing door knobs. ​(Enter your response rounded to the nearest whole​ number.)

Answer 1

The answer is "116 doorknobs".

Step-by-step explanation:

The standard deviation of the demand before the (four weeks) protection intervals =
`\sigma-d * (√(L)) = 100 \ units\\`

The desired cycle service level is
`99\%`.Therefore,
`z = 2.33`

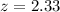
The safety stocks for the four-weeks protecting interval are:

Safety stock
`= z* [ \sigma-d * (√(L))]`

`= 2.33 * 100 \\\\= 233\ door\ knobs`

The safety stocks require for the one-week protection interval are:
`\sigma-dLT = \sigma-dt * (√(L)) = \sigma-dt * (√(4)) = 100\ door\ knobs\\\\\sigma-d = (100)/((√(4))) = (100)/(2) = 50 \ door\ knobs\\\\`

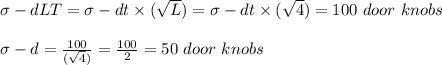
Safety stock
`= z* \sigma-dt = 2.33 * 50 = 116.5 \ or\ 117 \ door\ knobs\\\\`

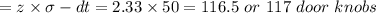
Safety stock reduction
`= 233 -117 = 116 \ door\ knobs`