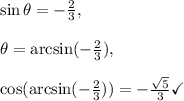Answer:

Explanation:
Draw a right triangle with angle
 . In all right triangles, the sine of an angle is equal to its opposite side divide by the hypotenuse of the triangle. Therefore, label the side opposite to
. In all right triangles, the sine of an angle is equal to its opposite side divide by the hypotenuse of the triangle. Therefore, label the side opposite to
 as 2 and the hypotenuse (longest side) of the right triangle as 3.
as 2 and the hypotenuse (longest side) of the right triangle as 3.
To find the last side, use the Pythagorean Theorem:
 , where
, where
 is the hypotenuse of the triangle.
is the hypotenuse of the triangle.
Solving for
 :
:

In all right triangles, the cosine of an angle is equal to its adjacent side divided by the hypotenuse. However, the cosine of all angles in Quadrant III are negative. Therefore, the desired answer is
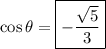 .
.
Verify: