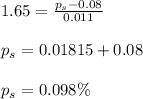Question

4. The legal limit for intoxication in Texas is 0.08% blood alcohol concentration (BAC) Suppose that a driver was tested with a breathalyzer that is subject to the standard error sigma approx0.011% . Answer the following problems using the normal approximation .

4(a) the breathalyzer reading was 0.085% , what is probability that the driver was not legally

4(b) the police officer wants to be at least 95% sure of DUI before arresting a suspected driver , at least how much BAC should he expect from his breathalyzer ?

Answer 1

The answer is below

Step-by-step explanation:

The z score is a score used to determine by how many standard deviations the raw score is above or below the mean. The z score is given by:

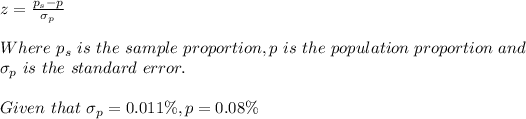
`z=(p_s-p)/(\sigma_p) \\\\Where\ p_s\ is\ the \ sample\ proportion, p\ is\ the\ population\ proportion\ and\\\sigma_p\ is\ the\ standard\ error.\\\\Given\ that\ \sigma_p=0.011\%,p=0.08\%`

a)

`For\ p_s=0.085\%\\\\z=(0.085-0.08)/(0.011) =0.45`

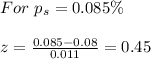
From the normal distribution table, P(z > 0.45) = 1 - 0.6736 = 32.64%

b) The z score that corresponds to a probability of 95% is 1.65

Therefore:

`1.65=(p_s-0.08)/(0.011) \\\\p_s=0.01815+0.08\\\\p_s=0.098\%`