Question

A force of 4 pounds is required to hold a spring stretched 0.4 feet beyond its natural length. How much work (in foot-pounds) is done in stretching the spring from its natural length to 0.6 feet beyond its natural length

Answer 1

the work done in stretching the spring from its natural length is -1.8 ft.lb

Explanation:

Given the data in the question;

From Hook's law, the magnitude of force applied on a spring is expressed as follows;

|F| = k|x|

where F is the force applied the spring, k is the spring constant, x is the length extension

Now, given that; F = 4 pounds = 4 lb and x = 0.4 ft

we substitute

4 = k × 0.4

k = 4 / 0.4

k = 10 lb/ft

Also, Hook's law can be expressed as follows;

F = -kx ---------- let this be equation 1

Now, work done by a force applied between two points is expressed as follows;

dW = Fdx ----------- let this be equation 2

substitute equation 1 into equation 2

dW = (-kx )dx

we integrate both side

∫(dW) = ∫((-kx )dx)

W = -k∫xdx

W = -k
`(x^2)/(2)`

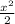
w = -
`(1)/(2)`kx²

we substitute 10 lb/ft for k and 0.6 ft for x

w = -
`(1)/(2)` × 10 lb/ft × (0.6 ft)²

w = -
`(1)/(2)` × 10 lb/ft × 0.36 ft²

w = -1.8 ft.lb

Therefore, the work done in stretching the spring from its natural length is -1.8 ft.lb