Question

A buffer solution contains 0.475 M nitrous acid and 0.302 M sodium nitrite . If 0.0224 moles of potassium hydroxide are added to 150 mL of this buffer, what is the pH of the resulting solution

Answer 1

Answer: The pH of the resulting solution will be 3.001

Step-by-step explanation:

Molarity is calculated by using the equation:

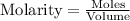`\text{Molarity}=\frac{\text{Moles}}{\text{Volume}}` ......(1)

We are given:

Moles of NaOH = 0.0224 moles

Molarity of nitrous acid = 0.475 M

Molarity of sodium nitrite = 0.302 M

Volume of solution = 150 mL = 0.150 L (Conversion factor: 1 L = 1000 mL)

Putting values in equation 1, we get:

`\text{Moles of nitrous acid}=(0.475mol/L* 0.150L)=0.07125mol`

`\text{Moles of sodium nitrite}=(0.302mol/L* 0.150L)=0.0453mol`

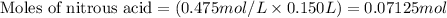
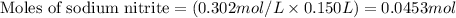
The chemical equation for the reaction of nitrous acid and NaOH follows:

`HNO_2+NaOH\rightleftharpoons NaNO_2+H_2O`

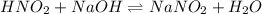
I: 0.07125 0.0224 0.0453

C: -0.0224 -0.0224 +0.0224

E: 0.04885 - 0.0677

The power of the acid dissociation constant is the negative logarithm of the acid dissociation constant. The equation used is:

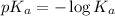`pK_a=-\log K_a` ......(2)

We know:

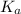`K_a` for nitrous acid =
`7.2* 10^(-4)`

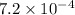
Using equation 2:

`pK_a=-\log (7.2* 10^(-4))=3.143`

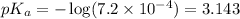
To calculate the pH of the acidic buffer, the equation for Henderson-Hasselbalch is used:

`pH=pK_a+ \log \frac{\text{[conjugate base]}}{\text{[acid]}}` .......(3)

Given values:

`[NaNO_2]=(0.0677)/(0.150)`

`[HNO_2]=(0.04885)/(0.150)`

`pK_a=3.143`

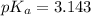
Putting values in equation 3. we get:

`pH=3.143-\log ((0.0677/0.150))/((0.04885/0.150))\\\\pH=3.143-0.142\\\\pH=3.001`

Hence, the pH of the resulting solution will be 3.001