Question

A spherical shell has an outside radius of 2.60 cm and an inside radius of a. The shell wall has uniform thickness and is made of a material with density 4.70 g/cm3. The space inside the shell is filled with a liquid having a density of 1.23 g/cm3. (a) Find the mass m of the sphere, including its contents, as a function of a. (b) In the answer to part (a), if a is regarded as a variable, for what value of a does m have its maximum possible value

Answer 1

The answer is below

Step-by-step explanation:

a) The volume of a sphere is:

Volume = (4/3)πr³; where r is the radius of the shell.

Given the outside radius of 2.60 cm and inner radius of a cm, the volume of the spherical shell is:

Volume of spherical shell =
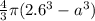`(4)/(3) \pi (2.6^3-a^3)` cm³

But Density = mass / volume; Mass = density * volume.

Therefore, mass of spherical shell = density * volume

mass of spherical shell =
`4.70\ g/cm^3` *
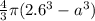`(4)/(3) \pi (2.6^3-a^3)` cm³

Mass of liquid = volume of inner shell * density of liquid

Mass of liquid =
`(4)/(3) \pi a^3\ cm^3*1.23\ g/cm^3`

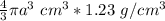
Total mass of sphere including contents = mass of spherical shell + mass of liquid

Total mass of sphere including contents (M) =
`4.70\ g/cm^3` *
`(4)/(3) \pi (2.6^3-a^3)\ cm^3` +
`(4)/(3) \pi a^3\ cm^3*1.23\ g/cm^3` =

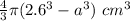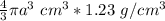Total mass of sphere including contents (M) = (346 - 14.5a³) grams

b) The mass is maximum when the value of a = 0

M = 346 - 14.5a³

M' = 43.5a² = 0

43.5a² = 0

a = 0