Question

Use implicit differentiation to find an equation of the tangent line to the curve at the given point. y2(y2 − 4) = x2(x2 − 5) (0, −2) (devil's curve)

Answer 1

Explanation:

Given that:

`y^2 (y^2-4) = x^2(x^2 -5)`

at point (0, -2)

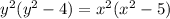
`\implies y^4 -4y^2 = x^4 -5x^2`

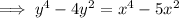
Taking the differential from the equation above with respect to x;

`4y^3 (dy)/(dx)-8y (dy)/(dx)= 4x^3 -10x`

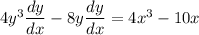
Collect like terms

`(4y^3 -8y)(dy)/(dx)= 4x^3 -10x`

`(dy)/(dx)= (4x^3 -10x)/(4y^3-8y)`

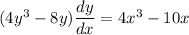
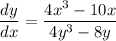
Hence, the slope of the tangent line m can be said to be:

`(dy)/(dx)= (4x^3 -10x)/(4y^3-8y)`

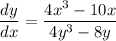
At point (0,-2)

`(dy)/(dx)= (4(0)^3 -10(0))/(4(-2)^3-8-(2))`

`(dy)/(dx)= (0 -0)/(4(-8)+16)`

`(dy)/(dx)= 0`

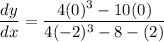
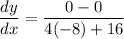
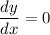
m = 0

So, we now have the equation of the tangent line with slope m = 0 moving through the point (x, y) = (0, -2) to be:

(y - y₁ = m(x - x₁))

y + 2 = 0(x - 0)

y + 2 = 0

y = -2