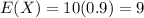Answer:
a) 38.74% probability that the main printer is operating properly for exactly 9 inspections.
b) Approximately 100% probability that the main printer is operating properly for at least 3 inspections.
c) The expected number of inspections in which the main printer is operating properly is 9.
Explanation:
For each inspection, there are only two possible outcomes. Either it is operating correctly, or it is not. The probability of the printer operating correctly for an inspection is independent of any other inspection, which means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
Based on past experience, the main printer in a university computer centre is operating properly 90% of the time.
This means that
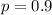
Suppose inspections are made at 10 randomly selected times.
This means that

A) What is the probability that the main printer is operating properly for exactly 9 inspections.
This is
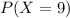 . So
. So

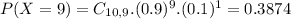
38.74% probability that the main printer is operating properly for exactly 9 inspections.
B) What is the probability that the main printer is operating properly for at least 3 inspections?
This is:
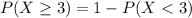
In which

So

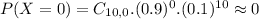
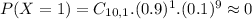

Thus:

Then:
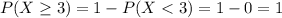
Approximately 100% probability that the main printer is operating properly for at least 3 inspections.
C) What is the expected number of inspections in which the main printer is operating properly?
The expected value for the binomial distribution is given by:
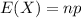
In this question: