Question

A boy standing throws a penny horizontally at 7.25 m/s out of the window of his apparent buliding. If the window is 10.0 m above the ground, how far from the base of the building does the penny land?

Answer 1

Step-by-step explanation:

This is a 2D problem (parabolic) so we have to think that way. We have to split up the problem into its 2 dimensions to solve it. Think "y-stuff" and "x-stuff".

In the y-stuff category:

v₀ = 0 (initial upwards velocity is 0 since we are told the penny is thrown horizontally)

Δx = -10.0 m (this displacement is negative because the penny lands 10.0 m below the point from which it was thrown)

a = -9.8 m/s/s

t = ? (we need to find the time in this dimension so we can use it in the x dimension to find the displacement, our unknown)

In the "x-stuff" category:

v₀ = 7.25 m/s (this is given)

Δx = ???

a = 0 (acceleration in this dimension is ALWAYS 0)

t = (we will solve for this in the y-dimension and plug it in here).

In the y dimension:

Δx = v₀t +
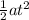`(1)/(2)at^2` and plugging in from the y-dimension info:

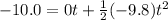`-10.0=0t+(1)/(2)(-9.8)t^2` which simplifies to

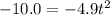`-10.0=-4.9t^2` so

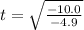`t=\sqrt{(-10.0)/(-4.9) }` which, to 2 significant digits is

t = 1.4 seconds

Now we will do the same in the x-dimension, using t = 1.4:

Δx = v₀t +
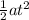`(1)/(2)at^2` and filling in the x-stuff:

Δx =
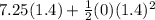`7.25(1.4)+(1)/(2)(0)(1.4)^2` Notice that the stuff after the + sign goes to 0 cuz of the multiplication of 0, so what we are left with is another form of the d = rt equation:

Δx = 7.25(1.4) + 0 so

Δx = 1.0 × 10¹ m (That's rounded correctly to 2 sig dig's: 10 m from the base of the building).

Answer 2

30.2

Step-by-step explanation: