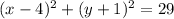Answer:
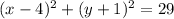
Explanation:
We want to find a circle whose diameter has the endpoints (6, 4) and (2, -6).
Since this is the diameter, its midpoint will be the center of the circle. Find the midpoint:
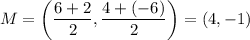
So, the center of our circle is (4, -1).
Next, to find the radius, we can find the length of the diameter and divide it by half.
Using the distance formula, find the length of the diameter:
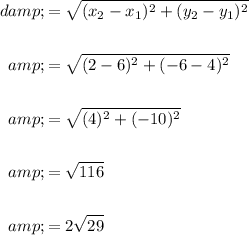
So, the radius will be:
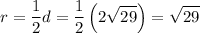
The equation for a circle is given by:
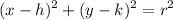
Substitute: