Question

HELP:Joyce is dividing into the water. Let the t represent time in seconds and the

h represent height in feet. Her dive is modeled by the equation:
h
-t2 + 10t + 19
You must show all your work on the scratch paper to receive full credit.
1. What is the height of the dividing board where Joyce is standing?
2. How many seconds will it take the diver to reach the maximum height?
3. How high is the maximum height of the diver?
EXPLAIN

Answer 1

Part 1)

The height of the diving board is 19 feet.

Part 2)

Five seconds.

Part 3)

44 feet.

Explanation:

Joyce's dive is represented by the equation:

`h=-t^2+10t+19`

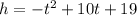
Where h represents her height (in feet) after t seconds.

Part 1)

Joyce is on the diving board right before she jumps. Therefore, to find the height of the diving board, we can let t = 0, since this is before she had jumped. Hence:

`h(0)=-(0)^2+10(0)+19=19\text{ feet}`

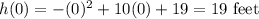
The height of the diving board is 19 feet.

Part 2)

Since this is a quadratic, the maximum height will occur at its vertex point.

So, we need to find the vertex. We can use the following formulas:

`\displaystyle \text{Vertex}=\left(-(b)/(2a), f\left(-(b)/(2a)\right)\right)`

In this case, a = -1, b = 10, and c = 19.

So, the t-coordinate of the vertex is:

`\displaystyle t=-((10))/(2(-1))=5\text{ seconds}`

Joyce will reach her maximum height after five seconds.

Part 3)

To find the maximum height, simply substitute this value back into the equation. Hence:

`h(5)=-(5)^2+10(5)+19=44\text{ feet}`

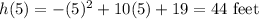
So, her maximum height is 44 feet in the air.