Question

This question is from the similarity chapter. It would be really kind of you if you would answer this question.

Answer 1

a) 1650 m

b) 1677.05 m

Explanation:

Hi there!

1) Determine what is required for the answers

For part A, we're asked for solve for the horizontal distance in which the road will rise 300 m. In other words, we're solving for the distance from point A to point C, point C being the third vertex of the triangle.

For part B, we're asked to solve for the length of the road, or the length of AB.

2) Prove similarity

In the diagram, we can see that there are two similar triangles: Triangle AXY and ABC (please refer to the image attached).

How do we know they're similar?

1. Angles AYX and ACB are corresponding and they both measure 90 degrees
2. Both triangles share angle A

Therefore, the two triangles are similar because of AA~ (angle-angle similarity).

3) Solve for part A

Recall that we need to find the length of AC.

First, set up a proportion. XY corresponds to BC and AY corresponds to AC:

`(XY)/(BC)=(AY)/(AC)`

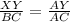
Plug in known values

`(2)/(300)=(11)/(AC)`

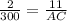
Cross-multiply

`2AC=11*300\\2AC=3300\\AC=1650`

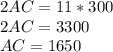
Therefore, the road will rise 300 m over a horizontal distance of 1650 m.

4) Solve for part B

To find the length of AB, we can use the Pythagorean theorem:

`a^2+b^2=c^2` where c is the hypotenuse of a right triangle and a and b are the other sides

Plug in 300 and 1650 as the legs (we are solving for the longest side)

`300^2+1650^2=c^2\\300^2+1650^2=c^2\\2812500=c^2\\1677.05=c`

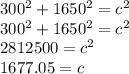
Therefore, the length of the road is approximately 1677.05 m.

I hope this helps!