Answer:
6 times
Explanation:
Given
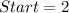
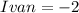 ---- i.e. multiplies by -2
---- i.e. multiplies by -2
 --- i.e. multiplies by 2
--- i.e. multiplies by 2
 --- signals
--- signals
Required
Number of times they have the same number
First, we list out all results of Ivan calculations.
To calculate Ivan's list, we simply multiply the current term by -2.
The 10 signals together with the first term, means there will be 11 terms in total
So, we have:
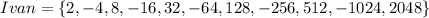
Next, list Adeline's

Compare the elements of the two lists, we have:
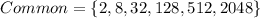
Hence, they have the same number 6 times.