Answer:
Step-by-step explanation:
From the information given:
The first thing is to calculate the total cost:
The total cost = fixed cost + Variable cost
= 55000 + 50Q
The total revenue TR = Price (P) × Demand (Q)
= (150 - 0.02Q) × Q
= 150Q - 0.02Q²
The marginal revenue MR =
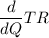
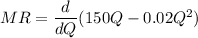
MR = 150 - 0.04Q
The marginal cost
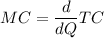
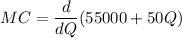
MC = 50
Now, the profit can be accomplished at the point when marginal revenue is equivalent to the marginal cost.
Then;
MR = MC
150 - 0.04Q = 50
-0.04Q = -150 + 50
-0.04 Q = -100
Q = 100/0.04
Q = 2500
Replacing the value of Q into P =150 - 0.02Q
P = 150 - 0.02(2500)
P = 150 - 50
P = $100
So, Profit = Total revenue - Total cost
Profit = (150Q - 0.02Q²) - ( 55000 + 50Q)
Profit = (150Q - 0.02Q² - 55000 - 50Q
Profit = 100Q - 0.02Q² - 55000
Profit = 100(2500) - 0.02(2500)² - 55000
Profit = 250000 - 125000 - 55000
Profit = $70000