Answer:
90°
Explanation:
There's are supplementary angles at point C. These are two angles that add up to 180°. We know this because a straight line makes 180° on both sides. Since we know that the first angle is 150°, we can determine the angle a point C is 30°. This is shown by:
180-150=30
So now we know 1 angle and the other two angles are put into like terms (in this case, multiples of x). It is known that the sum of all angles in a triangle equates to 180°. Using this information we can set up a simple equation.
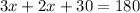
Combining like terms, we get:

Isolating x, we get:
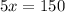
Dividing both sides by 5, we get:
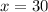
So now we can use this x-value to determine the angle that is being asked. It is shown that angle ABC is equal to 3x. Using the x value we just calculated, we get a final answer of:
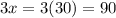
Therefore, the answer is 90°. Hope this helps!