Question

Write an equation to model the given scenario, then solve:

Each year the local country club sponsors a tennis tournament. Play starts with 128 participants. During each
round, half of the players are eliminated. How many players remain after 5 rounds?

Answer 1

Given:

Initial number of participants = 128

During each round, half of the players are eliminated.

To find:

The number of players remain after 5 rounds.

Solution:

It is given that, the initial number of participants is 128 and during each round, half of the players are eliminated.

If half of the players are eliminated, then half of the players are remained.

So, the initial value is 128 and the decay factor is
`(1)/(2)`.

The general exponential decay model is:

`y=a(b)^x`

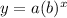
Where, a is the initial value and b is the decay factor.

Putting
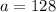`a=128` and
`b=(1)/(2)` in the above model, we get

`y=128\left((1)/(2)\right)^x`

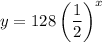
Here, y is the number of remaining players after x rounds.

Substituting
`x=5`, we get

`y=128\left((1)/(2)\right)^5`

`y=128\left((1)/(32)\right)`

`y=4`

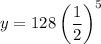
Therefore, the required model is
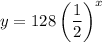`y=128\left((1)/(2)\right)^x` and the number of players remain after 5 rounds is 4.