Answer:
option D
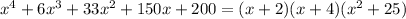
Explanation:
Since no factors are mentioned at all. We use trial and error method to find a root of the polynomial.
Step 1 :
For that we will consider the factors of 200 :
± 1 , ±2, ± 4, ±5, ±8, ±10, ±20, ±25, ±40, ±50, ±100, ±200
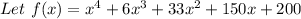
f ( -1 ) = (-1)⁴ + 6 (-1)³ + 33(-1)² + 150(-1) + 200
= 1 - 6 + 33 - 150 + 200
= 78 ≠ 0
So - 1 is not a root.
f ( - 2) = ( -2)⁴ + 6( - 2 )³ + 33 (- 2) ² + 150 (- 2) + 200
= 16 - 48 + 132 - 300 + 200
= 0
Therefore - 2 is a root of f( x ) and ( x + 2) is a factor of f( x) .
Step 2
Now we will use synthetic division to find other factors.
-2 | 1 6 33 150 200
| 0 -2 -8 -50 -200
|_______________________________
1 4 25 100 0
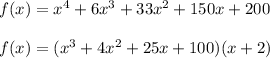
We will use trial and error method again to further factorize the equation
g(x) = x³ + 4x² + 25x +100.
Proceed as in step 1
Consider the factors of 100 to find the root.
Factors of 100 :±1, ±2, ±4 , ±5 , ±8, ±10 , ± 20, ±25, ± 50, ±100
g( - 4) = ( -4)³ + 4 ( -4)² + 25(-4) + 100
= - 64 + 64 - 100 + 100
= 0
Therefore - 4 is a root of g(x) , that means (x + 4) is a factor.
Now we will use synthetic division :
- 4 | 1 4 25 100
| 0 -4 0 -100
|_____________________
1 0 25 0
Therefore g(x) = ( x² + 0x + 25)(x + 4)
= ( x² + 25 )( x + 4)
Therefore the factorized form of
x⁴ + 6x³ + 33x² + 150x + 200 = (x + 2)(x³ + 4x² + 25x + 100)
= ( x + 2 )( x + 4 )( x² + 25)