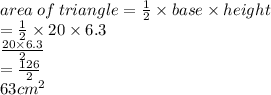Question

IB QUESTIONS:

The height of a vertical cliff is 450 m. The angle of elevation from a ship to
the top of the cliff is 31°. The ship is x metres from the bottom of the cliff.
a Draw a diagram to show this information.
b Calculate the value of x.
In the diagram, triangle ABC is isosceles.
AB = AC, CB = 20 cm and angle ACB is 32º.
Find a the size of angle CAB
b the length of AB
c the area of triangle ABC.
30
200

Answer 1

Explanation:

Using SOHCAHTOA

`\tan = (opposite)/(adjacent) \\ \tan {31}^(0) = (450)/(x) \\ \tan {31}^(0) = 0.6009 \\ 0.6009 = (450)/(x) \\ cross \: multiply \\ 0.6009x = 450 \\ divide \: both \: sides \: by \: 0.6009 \\ x = (450)/(0.6009)x \\ = 748.9`

Second Question Explanation:

a. The base angles of an isosceles triangle are equal so angle ABC is also 32°

but the sum of angles in a triangle = 180° therefore

let angle CAB be x

`{32}^(0) + {32}^(0) + {x}^(0) = {180}^(0) \\ 64 + x = 180 \\ {x}^(0) = 180 - 64 \\ {x}^(0) = {116}^(0)`

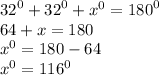
b. If you share a triangle in half you get 2 right angles so I'll use SOHCAHTOA to find the length AB

First the base of the right angled triangle will be 20/2 = 10

`\cos = (adjacent)/(hypotenuse) \\ \cos {32}^(0) = (10)/(ab) \\ \cos32 = 0.8480 \\ 0.8480 = (10)/(ab) \\ ab = (10)/(0.8480) \\ line \: ab = 11.8`

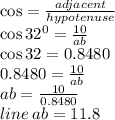
c. To find the are we'll need to get the height first

using the right angled triangle With base 10cm and hypotenuse 11. 8 to find the height we'll use the Pythagorean theorem

`{(11.8)}^(2) = {x}^(2) + {10}^(2) \\ 1324.24 = {x}^(2) + 100 \\ {x}^(2) = 139.24 - 100 \\ {x}^(2) = 39.24 \\ \sqrt{ {x}^(2) } = √(39.24) \\ x = √(39.24 ) \\ x = 6.3`

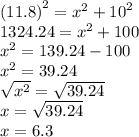
now to find the area

`area \: of \: triangle = (1)/(2) * base * height \\ = (1)/(2) * 20 * 6.3 \\ (20 * 6.3)/(2) \\ = (126)/(2) \\ 63 {cm}^(2)`