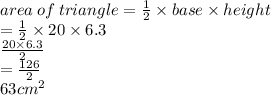Explanation:
Using SOHCAHTOA

Second Question Explanation:
a. The base angles of an isosceles triangle are equal so angle ABC is also 32°
but the sum of angles in a triangle = 180° therefore
let angle CAB be x
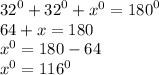
b. If you share a triangle in half you get 2 right angles so I'll use SOHCAHTOA to find the length AB
First the base of the right angled triangle will be 20/2 = 10
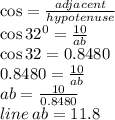
c. To find the are we'll need to get the height first
using the right angled triangle With base 10cm and hypotenuse 11. 8 to find the height we'll use the Pythagorean theorem
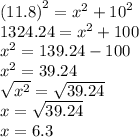
now to find the area