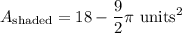Question

Find the area of the shaded region. Leave your answer in terms of pi.

Answer 1

`\displaystyle A_\text{shaded}=18-(9)/(2)\pi \text{ units}^2`

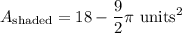
Explanation:

First, find the area of the rectangle:

`A_\text{rect}=9(3)=18\text{ units}^2`

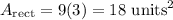
In order to find the area of the shaded region, we can subtract the areas of the two sectors from the total area of the rectangle.

Find the area of the sectors. We can use the sector formula:

`\displaystyle A=\pi r^2\cdot (\theta)/(360^\circ)`

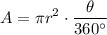
The left sector has a radius of three units and an angle of 90°. Hence, its area is:

`\displaystyle A_\text{L}=\pi (3)^2\cdot (90)/(360)=9\pi\cdot (1)/(4)=(9)/(4)\pi`

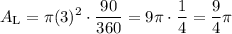
The right sector is identical to the left sector. So, the total area of the two sectors is:

`\displaystyle A_{\text{T}}=(9)/(4)\pi +(9)/(4)\pi =(9)/(2)\pi`

Hence, the area of the shaded region is:

`\displaystyle A_\text{shaded}=18-(9)/(2)\pi \text{ units}^2`