Question

Two sides of a triangle are perpendicular. If the two sides are 8cm and 6cm, calculate correct to the next degree, the smallest angle of the triangle. (A)35° (B)36° (C)37° (D)38° (E)53°​

Answer 1

`\boxed{Given:}`

Length of the perpendicular ( opposite ) = 6 cm.

Length of the base ( adjacent ) = 8 cm.

`\boxed{To\:find:}`

The smallest angle of the triangle.

`\boxed{Solution:}`

`\sf\purple{C.\:37°}` ✅

`\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\red{:}}}}}`

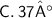In a right-angled triangle, if two sides are given, the measure of the unknown angle can be known.

Since the value of opposite and adjacent sides are given, we use the tangent formula.

tan θ =
`(opposite)/(adjacent)`

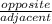
✒ tan θ =
`(6 \: cm)/(8 \: cm)`

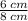
✒ θ =
`{tan}^( - 1)` (0.75)

✒ θ = 36.9°

✒ θ = 37°

Now let us find the other unknown angle 'x'.

We know that,

Sum of angles of a triangle = 180°

✒ 37° + x + 90° = 180° (90° since it is a right-angled triangle)

✒ x + 127° = 180°

✒ x = 180° - 127°

✒ x = 53°

Therefore, the three angles of the triangle are 37°, 53° and 90°.

Hence, the smallest angle is 37°.

`\huge{\textbf{\textsf{{\orange{My}}{\blue{st}}{\pink{iq}}{\purple{ue}}{\red{35}}{\green{♡}}}}}`