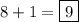Question

A group of 35 team members needs to be divided into smaller workgroups. If each group is to contain two, three, or four people, what is the smallest number of groups possible?

Answer 1

The answer is 9
Sorry if I get it wrong

Answer 2

9

Explanation:

Since we want the fewest number of groups possible, we need to maximize the number of people in each group. Since there can be a maximum of four people in each group, we can have a maximum of
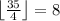`\left\lfloor (35)/(4)\right \rfloor=8` groups of four. The final three students can form the last group, hence the smallest number of groups possible is
`8+1=\boxed{9}`