Question

MCR3U1 Culminating 2021.pdf

#7.
A colony of bacteria is introduced into a growth medium. Its initial population
size is 350 thousand. 12 hours later, the colony has grown to a size of
800 thousand. If its population size increases exponentially, determine:
(a)
the exponential growth model for the size of the population Alt), after
t hours.
(b)
the population size after (i) 8 hours and (ii) 24 hours.
(c)
the rate of increase in the population size as a %/hour
(d)
the doubling time of the bacteria population.​

Answer 1

(a)
`y = 350,000 * (1 + 0.07132)^t`

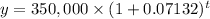
(b) (i) The population after 8 hours is 607,325

(ii) The population after 24 hours is 1,828,643

(c) The rate of increase of the population as a percentage per hour is 7.132%

(d) The doubling time of the population is approximately, 10.06 hours

Explanation:

(a) The initial population of the bacteria, y₁ = a = 350,000

The time the colony grows, t = 12 hours

The final population of bacteria in the colony, y₂ = 800,000

The exponential growth model, can be written as follows;

`y = a \cdot (1 + r)^t`

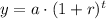
Plugging in the values, we get;

`800,000 = 350,000 * (1 + r)^(12)`

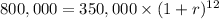
Therefore;

(1 + r)¹² = 800,000/350,000 = 16/7

12·㏑(1 + r) = ㏑(16/7)

㏑(1 + r) = (㏑(16/7))/12

r = e^((㏑(16/7))/12) - 1 ≈ 0.07132

The model is therefore;

`y = 350,000 * (1 + 0.07132)^t`

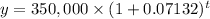
(b) (i) The population after 8 hours is given as follows;

y = 350,000 × (1 + 0.07132)⁸ ≈ 607,325.82

By rounding down, we have;

The population after 8 hours, y = 607,325

(ii) The population after 24 hours is given as follows;

y = 350,000 × (1 + 0.07132)²⁴ ≈ 1,828,643.92571

By rounding down, we have;

The population after 24 hours, y = 1,828,643

(c) The rate of increase of the population as a percentage per hour = r × 100

∴ The rate of increase of the population as a percentage = 0.07132 × 100 = 7.132%

(d) The doubling time of the population is the time it takes the population to double, which is given as follows;

Initial population = y

Final population = 2·y

The doubling time of the population is therefore;

`2 \cdot y = y * (1 + 0.07132)^t`

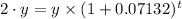
Therefore, we have;

2·y/y =2 =
`(1 + 0.07132)^t`

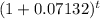
t = ln2/(ln(1 + 0.07132)) ≈ 10.06

The doubling time of the population is approximately, 10.06 hours.