Question

The midterm grades for two high school algebra classes are provided in the tables below. For convenience, the data have been ordered.

Class 1: 72 73 74 75 76 79 82 83 84 86 91
92 93 93 94 95 97 97 98 98
Class 2: 59 65 68 69 72 73 78 80 82 82
83 83 85 88 88 89 94 96 97 98
A. Sketch parallel boxplots for the two classes.
B. Which class has the better overall performance? Justify your answer.
C. The teacher for the two classes calculates a 90% confidence interval for the difference in mean midterm grades between Class #1 and Class #2. The confidence interval is (0.09299, 11.413). Assume that confidence interval conditions are met. Based on the confidence interval, do you think there is a difference in the population mean midterm grades for the two classes? Explain.

Answer 1

Following are the responses to the given question:

Explanation:

For point a:

In R-Studio, we first insert the data set,

Please notice that perhaps the blue colored lines are input and the green lines are R-Studio results.

`Class \ 1 = c(72,73,74,75,76,79,82,83,84,86,91,92,93,93,94,95,95,97,98,98)\\\\Class\ 2 = c(59,65,68,68,69,72,73,78,80,82,82,83,83,85,88,88,89,94,96,97,98)`

We will get the smallest observation, first, mid, third, and largest quartile for both classes and use a summary of 5 numbers,

`\to five\ num(Class\ 1) \\\\\[1\] \ 72.0 77.5 88.5 94.5 98.0 \\\\\to five\ num(Class\ 2) \\\\\[1\]\ 59 72 82 88 98`

The table can be defined as follows:

`Class\ 1\ \ \ \ \ \ \ \ \ \ \ \ Class\ 2 \\`

`Smallest \ value\ \ \ \ \ \ \ 72\ \ \ \ \ \ \ 59\\First \ quartile \ Q1\ \ \ \ \ \ \ 77.5\ \ \ \ \ \ \ 72\\Median\ Q2 \ \ \ \ \ \ \ 88.5\ \ \ \ \ \ \ 82\\Third \ quartile \ Q3 \ \ \ \ \ \ \ 94.5\ \ \ \ \ \ \ 88\\Largest \ value \ \ \ \ \ \ \ 98\ \ \ \ \ \ \ 98\\`

The parallel boxplots in R-Studio as,

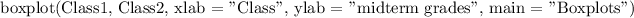`\text{boxplot(Class1, Class2, xlab =`Please find the graph file.

For point b:

Its performance overall of Class 1 is better, while the median of class 1 is greater than class 2, as well as the value (grades) of class 1, is less dispersed in relation to class 2.

For point c:

The stated 90 percent confidence interval for a significant difference is (0.09299, 11.413) Users now calculate the difference among Class 1 and Class 2 plan presented of mean value as:

`mean \ (Class \ 1) \\\\\[1\]\ 86.5\\\\mean\ (Class\ 2)\\\\`

`\[ 1 \] \ 80.80952\\\\Difference = 86.5 - 80.80952 = 5.69048`

Its discrepancy among two estimations is between confidence interval of 90 percent (0.09299, 11.413). Its mean population of grades of two classes therefore differs significantly.