Question

Every day, Luann walks to the bus stop and the amount of time she will have to wait for the bus is between 0 and 12 minutes, with all times being equally likely (i.e., a uniform distribution). This means that the mean wait time is 6 minutes, with a variance of 12 minutes. What is the 25th percentile of her total wait time over the course of 60 days?

a. 341.902.
b. 349.661.
c. 363.372.
d. 378,099.

Answer 1

a. 341.902.

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

n instances of a normal variable:

For n instances of a normal variable, the mean is
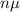`n\mu` and the standard deviation is
`s = \sigma√(n)`

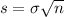
60 days, for each day, mean 6, variance of 12.

So

`\mu = 60*6 = 360`

`s = √(12)√(60) = 26.8328`

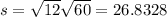
What is the 25th percentile of her total wait time over the course of 60 days?

X when Z has a p-value of 0.25, so X when Z = -0.675.

`Z = (X - \mu)/(s)`

`-0.675 = (X - 360)/(26.8328)`

`X - 360 = -0.675*26.8328`

`X = 341.902`

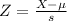
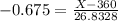
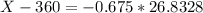
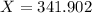
Thus, the correct answer is given by option A.