Answer:
a) 158.4 HP.
b) 1235.6 °F.
Step-by-step explanation:
Hello there!
In this case, according to the given information, it turns out possible for us to set up an energy balance for the turbine's inlets and outlets:
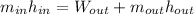
Whereas the mass flow is just the same, which means we have:
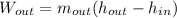
And the enthalpy and entropy of the inlet stream is obtained from steam tables:

Now, since we assume the 80% accounts for the isentropic efficiency for this adiabatic gas turbine, we assume the entropy is constant so that:
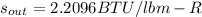
Which means we can find the temperature at which this entropy is exhibited at 15 psia, which gives values of temperature of 1200 °F (s=2.1986 BTU/lbm-K) and 1400 °F (s=2.2604 BTU/lbm-K), and thus, we interpolate for s=2.2096 to obtain a temperature of 1235.6 °F.
Moreover, the enthalpy at the turbine's outlet can be also interpolated by knowing that at 1200 °F h=1639.8 BTU/lbm and at 1400 °F h=174.5 BTU/lbm, to obtain:
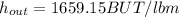
Then, the isentropic work (negative due to convention) is:
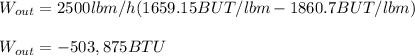
And the real produced work is:
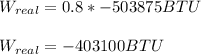
Finally, in horsepower:
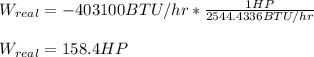
Regards!