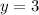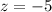Answer:

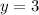
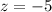
Explanation:
Given:
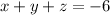


Solve for
 in the 1st equation:
in the 1st equation:
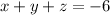
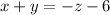
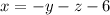
Substitute the value of
 into the 2nd equation and solve for
into the 2nd equation and solve for
 :
:

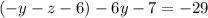

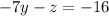
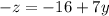
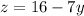
Substitute the value of
 into the 3rd equation and solve for
into the 3rd equation and solve for
 :
:

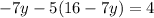
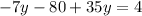
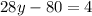

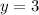
Plug
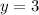 into the solved expression for
into the solved expression for
 and evaluate to solve for
and evaluate to solve for
 :
:

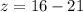
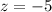
Plug
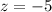 into the solved expression for
into the solved expression for
 and evaluate to solve for
and evaluate to solve for
 :
:

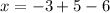
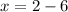

Therefore: