Question

Determine the solution set of x2 - 80 = 0.

{± }
{±4 }
{±2 }

Answer 1

Answer:
`\Big\{\pm 4√(5) \Big\}`

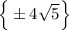
This is the shorthand way of writing
`\Big\{4√(5), -4√(5) \Big\}`

=====================================================

Work Shown:

`x^2 - 80 = 0\\\\x^2 = 80\\\\x = \pm√(80)\\\\x = \pm√(16*5)\\\\x = \pm√(16)*√(5)\\\\x = \pm4√(5)\\\\x = 4√(5) \ \text{ or } \ x = -4√(5)\\\\`

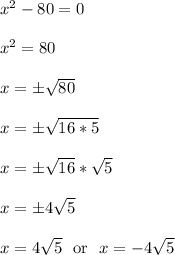
The plus or minus is needed because squaring a negative leads to a positive. As another example, x^2 = 25 has x = 5 and x = -5 as the two solutions. Note that x^2 = (-5)^2 = (-5)*(-5) = 25.

Also, note that the 80 was broken up into 16*5. This was done to simplify the square root. We pull out the largest factor that's a perfect square.

So that's how we get to the solution set
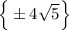`\Big\{\pm 4√(5) \Big\}`. The curly braces tell the reader that they are dealing with a set.