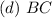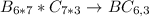Answer:
a. AB: 3 by 7
b. BA: N by N
c. A^TB: N by N
d. BC: 6 by 3
Explanation:
Given
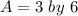
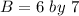
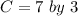
Required
The dimension of the following matrices
As a general rule:
For A * B to be successful, the columns in a must equal the rows in B
Using this rule, we have:

So:
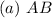

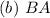
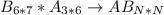
The column numbers of B does not equal the row numbers of A.
Hence, BA does not exist
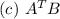
 implies that:
implies that:
If
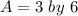 , then
, then
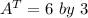
So:
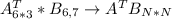
The column numbers of A^T does not equal the row numbers of B.
Hence,
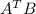 does not exist
does not exist