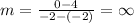Answer:
Table 1
Explanation:
The slope of a line (m) passing through two points A(x₁, y₁) and B(x₂, y₂) is given by:
m = (y₂ - y₁) / (x₂ - x₁)
a) From table 1, we can select two points. Let us select point (-3, 2) and point (1, 2). Hence the slope is:
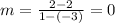
b) From table 2, we can select two points. Let us select point (-3, 3) and point (1, -1). Hence the slope is:
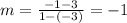
c) The graph passes through point (0, 0) and (3,3). Hence:

d) The graph passes through point (-2, 4) and (-2,0). Hence: