Question

What conclusions can be made about the amount of money in each account if f represents Molly's account and g represents her brother's account?

Answer 1

(b) is true

Explanation:

Given

Molly

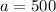`a = 500` --- starting balance

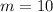`m = 10` --- monthly rate

Her brother

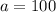`a = 100` ---- starting balance

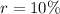`r = 10\%` --- annual rate

Required

Determine which option is true

First, we calculate her brother's function.

The function is an exponential function calculated as:

`y = ab^x`

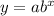
Where
`b = 1 + r`

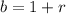
So, we have:

`y = ab^x`

`y = 100 *(1 + 10\%) ^x`

`y = 100 *(1 + 0.10) ^x`

`y = 100 *(1.10) ^x`

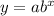
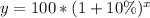
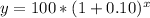
Hence:

`g(x) = 100 *(1.10) ^x`

Next, we calculate Molly's function (a linear function)

The monthly function is:

`y = mx + a`

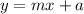
So, we have:

`y = 10x + 500`

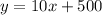
Annually, the function will be:

`y = 10x*12 + 500`

`y = 120x + 500`

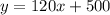
So, we have:

`f(x) = 120x + 500`

At this point, we have:

`f(x) = 120x + 500` ---- Molly

`g(x) = 100 *(1.10) ^x` ---- Her brother

Next, we test each option

(a): Molly's account will have a faster rate of change over [32,40]

We calculated Molly's function to be:

`y = 120x + 500`

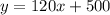
The slope of a linear function with the form:
`y = mx + b` is m

By comparison:

`m = 120`

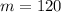
Since Molly's account is a linear function, the rate of change over any interval will always be the same; i.e.

`m = 120`

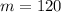
For his brother:

Rate of change is calculated using:

`m = (g(b) - g(a))/(b - a)`

`m = (g(40) - g(32))/(40 - 32)`

`m = (g(40) - g(32))/(8)`

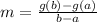
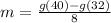
Calculate g(40) and g(32)

`g(x) = 100 *(1.10) ^x`

`g(40) = 100 * 1.10^(40) =4526`

`g(32) = 100 * 1.10^(32) = 2111`

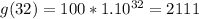
So, we have:

`m = (4526 - 2111)/(8)`

`m = (2415)/(8)`

`m = 302`

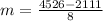
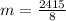
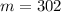
By comparison:
`302 > 120`

Hence, her brother's account has a faster rate over [32,40]

(a) is false

(b): Molly's account will have a slower rate of change over [24,30]

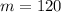`m = 120` --- Molly's rate of change

For his brother:

`m = (g(b) - g(a))/(b - a)`

`m = (g(30) - g(24))/(30 - 24)`

`m = (g(30) - g(24))/(6)`

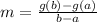
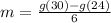
Calculate g(30) and g(24)

`g(x) = 100 *(1.10) ^x`

`g(40) = 100 * 1.10^(30) =1745`

`g(32) = 100 * 1.10^(24) = 985`

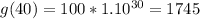
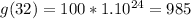
So, we have:

`m = (g(30) - g(24))/(6)`

`m = (1745 - 985)/(6)`

`m = (760)/(6)`

`m = 127`

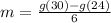
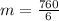
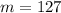
By comparison:
`127 > 120`

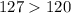
Hence, Molly's account has a slower rate over [24,30]

(b) is false

(c): Molly's account will have a slower rate of change over [0,4]

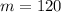`m = 120` --- Molly's rate of change

For his brother:

`m = (g(b) - g(a))/(b - a)`

`m = (g(4) - g(0))/(4 - 0)`

`m = (g(4) - g(0))/(4)`

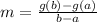
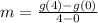
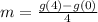
Calculate g(4) and g(0)

`g(x) = 100 *(1.10) ^x`

`g(4) = 100 * 1.10^4 =146`

`g(0) = 100 * 1.10^(0) = 100`

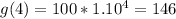
So, we have:

`m = (g(4) - g(0))/(4)`

`m = (146 - 100)/(4)`

`m = (46)/(4)`

`m = 11.5`

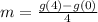
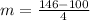
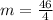
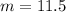
By comparison:
`120>11.5`

Hence, Molly's account has a faster rate over [0,4]

(c) is false