Answer:
a) B = 3.11 km. θ= 54.7º E of S
b) B = 3.11 km θ= 54.7º W of S
Step-by-step explanation:
a)
- Since we know the value of the total displacement, and the value of the displacement A and its direction, we can find the magnitude of B just applying the Pythagorean Theorem, as follows:
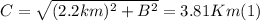
- Solving for B, the only unknown, we get:
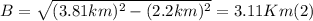
- Now, applying some simple trig, we can find the angle that (A+B) makes with the S axis, as follows:

- Since it's a positive number, applying the convention that the positive angles are measured counterclockwise, this means that this angle is measured East of South.
b)
- If the magnitude of A-B is the same than the one for A+B, this means that the magnitude of B remains the same, i.e. 3.11 Km.
- But if we do graphically A-B, as it is the same as adding A + (-B), we find that the angle of A-B is different to the one in A+B, even the magnitudes of both displacements are the same.
- In this case, B is a negative number, because it's a displacement due west.
- So, applying the same trig that for a) we can find the angle that (A-B) makes with the S Axis, as follows:

- So, since it is negative, it's measured clockwise from the S axis, so it's 54.7º W of S.