Answer:
The horizontal asymptote represents the terminal population of the trout.
Explanation:
The horizontal asymptote of the given rational function is the limit of
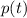 when
when
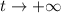 . That is:
. That is:
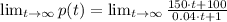 (1)
(1)
Then, we apply the concept of limits for rational-polynomial functions:
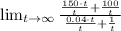
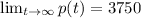
The horizontal asymptote represents the terminal population of the trout. In this case, the terminal population of the trout is 3750.