Answer:
The least amount of fencing needed for the rectangular pen is 72.19 feet.
Explanation:
The area and perimeter equations of the pen are, respectively:
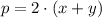 (1)
(1)
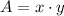 (2)
(2)
Where:
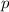 - Perimeter, in feet.
- Perimeter, in feet.
 - Area, in square feet.
- Area, in square feet.
 - Width, in feet.
- Width, in feet.
 - Length, in feet.
- Length, in feet.
Let suppose that total area is known and perimeter must be minimum, then we have a system of two equations with two variables, which is solvable:
From (2):

(2) in (1):
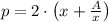
And the first and second derivatives of the expression are, respectively:
 (3)
(3)
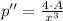 (4)
(4)
Then, we perform the First and Second Derivative Test to the function:
First Derivative Test
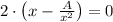
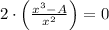
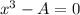
Given that dimensions of the rectangular pen must positive nonzero variables:
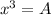
![x = \sqrt[3]{A}](https://img.qammunity.org/2022/formulas/mathematics/high-school/6ji0ua5xq8c96n3busz6e5guqxmegzw7hc.png)
Second Derivative Test

In a nutshell, the critical value for the width of the pen leads to a minimum perimeter.
If we know that
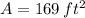 , then the value of the perimeter of the rectangular pen is:
, then the value of the perimeter of the rectangular pen is:
![x = \sqrt[3]{169\,ft^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/3q0g2a45oulxad99giycbym351cikxcz1b.png)
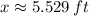
By (2):

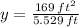
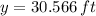
Lastly, by (1):
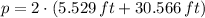
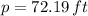
The least amount of fencing needed for the rectangular pen is 72.19 feet.