Answer:
Katie will catch up to Susan after running 33.4 h.
Explanation:
We can find the time that takes Katie to catch up to Susan by using the following equation:
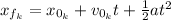
Where:
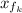 : is the final position of Katie
: is the final position of Katie
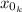 : is the initial position of Katie = 0
: is the initial position of Katie = 0
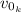 : is the initial speed of Katie = 5.2 mi/h
: is the initial speed of Katie = 5.2 mi/h
a: is the acceleration = 0 (she is moving at constant speed)
t: is the time
Since Katie will catch up to Susan, the final distance traveled by Katie will be equal to the final distance traveled by Susan.
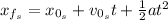

Since Susan gets a 45 minutes head start, in that time she traveled the following distance:

So, this will be the initial position of Susan.
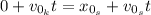
Hence, the time will be:
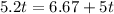
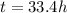
Therefore, Katie will catch up to Susan after running 33.4 h.
I hope it helps you!