Question

Quickbrush Paint Company is developing a linear program to determine the optimal quantities of ingredient A and ingredient B to blend together to make oil-base and water-base paint. The oil-base paint contains 90 percent A and 10 percent B, whereas the water-base paint contains 30 percent A and 70 percent B. Quickbrush currently has 10,000 gallons of ingredient A and 5,000 gallons of ingredient B in inventory and cannot obtain more at this time. Assuming that x represents the number of gallons of oil-base paint, and y represents the gallons of water-base paint, which constraint is correctly represents the constraint on ingredient A?

A. .9x + .3y ≤ 10,000
B. .9A + .1B ≤ 10,000
C. .9x + .1y ≤ 10,000
D. .3x + .7y ≤ 10,000

Answer 1

A. 0.9x + 0.3y ≤ 10,000

Step-by-step explanation:

Given

`x \to` oil based plant

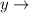`y \to` water based plant

The data can be represented in tabular form as:

`\begin{array}{ccc}{} & {A} & {B} & {x} & {90\%} & {10\%} & {y} & {30\%} & {70\%} & {} & {10000} & {5000}\ \end{array}`

Considering only A, we have the following constraints:

`A \to 90\% * x + 30\% * y`

`A \to 0.9x + 0.3y`

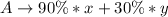
Since the company currently has 10000 of A.

The above constraint implies that, the mixture cannot exceed 10000.

So, we have:

`A \to 0.9x + 0.3y \le 10000`

Hence, (A) is correct