Question

The amount of radium 226 remaining in a sample that originally contained A grams is approximately C(t) = A(0.999 567)t. Where t is time in years find the half-life to the nearest 100 years

Answer 1

The half-life of the substance is of 1600 years.

Explanation:

Amount of the substance:

The amount of the substance after t years is given by the following equation:

`C(t) = A(0.999567)^t`

In which A is the initial amount.

Find the half-life:

This is t for which
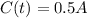`C(t) = 0.5A`, that is, the amount is half the initial amount. So

`C(t) = A(0.999567)^t`

`0.5A = A(0.999567)^t`

`(0.999567)^t = 0.5`

`\log{(0.999567)^t} = \log{0.5}`

`t\log{0.999567} = \log{0.5}`

`t = \frac{\log{0.5}}{\log{0.999567}}`

`t = 1600`

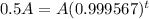
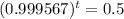
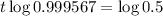
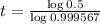
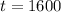
The half-life of the substance is of 1600 years.