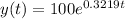Answer:
The number of bacteria after t hours is given by:
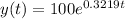
Explanation:
Amount of bacteria after t hours:
Is given by the following equation:
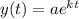
In which a is the initial value and k is the constant of growth.
There are 100 bacteria initially
This means that
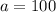 . So
. So
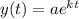
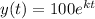
500 bacteria five hours later.
This means that
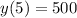 . We use this to find k. So
. We use this to find k. So
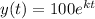
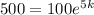
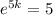
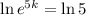
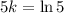
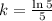
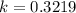
So
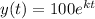
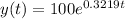
The number of bacteria after t hours is given by: