Question

What is the slope that passes through the points : (-2,9) and (4,-7)

Answer 1

y = -8 / 3x + 11/3

Explanation:

Using the slope formula:

`slope = y = ((y_(2)-y_(1)))/((x_(2)-x_(1)))`

1. Select one point to be
`(x_(1) ,y_(1) )` and the other
`(x_(2) ,y_(2) )`

I chose (-2, 9) to be
`(x_(1) ,y_(1) )` and (4, -7) to be
`(x_(2) ,y_(2) )`

2. Plug the values into the formula:

`y = (-7-9)/(4-(-2)) \\\\y= (-16)/(6) \\\\y = (-8)/(3)`

3. Finding the c-value by plugging in one of the points into the equation

y = mx + c

9 = -8/3 (-2) + c

9 = 16/3 + c

c = 11/3

4. y = -8/3x + 11/3

Answer 2

Use the slope formula below:

`\large \boxed{m = (y_2 - y_1)/(x_2 - x_1) }`

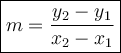
The m-term represents the slope.

The formula is the changes of two y-points over the changes of two x-points. We are given two points. Substitute both points in the formula.

`\large{m = (9 - ( - 7))/( - 2 - 4) } \\ \large{m = (9 + 7)/( - 6) \longrightarrow (16)/( - 6) } \\ \large{m = (8)/( -3 ) \longrightarrow - (8)/(3) }`

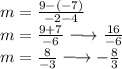
Therefore the slope is -8/3

Answer

• the slope is -8/3

Hope this helps! Let me know if you have any doubts.